Công thức tính tổng cấp số cộng
Để tính tổng n số hạng đầu tiên của một cấp số cộng, ký hiệu là Sn, chúng ta có hai cách tiếp cận chính. Cách thứ nhất được sử dụng khi bạn đã biết số hạng đầu tiên u1 và số hạng cuối cùng un của dãy. Công thức tính tổng cấp số cộng trong trường hợp này là: Sn = n * (u1 + un) / 2. Cách tính này dựa trên nguyên lý ghép cặp các số hạng đối xứng trong dãy số để tạo ra các tổng bằng nhau.
Tính tổng dựa trên số hạng đầu và công sai
Trong trường hợp không biết số hạng cuối cùng, bạn có thể tính Sn dựa vào số hạng đầu u1 và công sai d. Công thức tính tổng cấp số cộng biến đổi sẽ là: Sn = n * u1 + [n * (n - 1) * d] / 2. Công thức này rất hữu ích khi đề bài chỉ cung cấp quy luật tăng hoặc giảm của dãy số cùng với giá trị bắt đầu. Việc ghi nhớ cả hai dạng công thức giúp bạn linh hoạt hơn trong quá trình làm bài tập thực tế.
Giải thích các đại lượng trong công thức
Để áp dụng đúng công thức tính tổng dãy cấp số cộng, bạn cần xác định chính xác các đại lượng có mặt trong biểu thức. Trong đó, n là số lượng các số hạng tham gia vào tổng, u1 là giá trị của số hạng đầu tiên và d là khoảng cách giữa hai số liên tiếp (công sai). Chỉ cần nhầm lẫn một trong các yếu tố này, kết quả cuối cùng sẽ hoàn toàn sai lệch. Do đó, bước xác định giả thiết luôn là bước quan trọng nhất trước khi đặt bút tính toán.

Hai dạng biểu thức phổ biến để tính tổng dãy số cấp số cộng
Nhiều bài toán không cho sẵn n, buộc bạn phải tìm ra số lượng số hạng trước khi áp dụng công thức tính tổng dãy cấp số cộng. Công thức để tìm n khi biết số đầu u1, số cuối un và công sai d là: n = (un - u1) / d + 1. Đây là bước đệm không thể thiếu trong các bài toán tính tổng của một dãy số tự nhiên cách đều dài. Nếu n không phải là một số nguyên dương, bạn cần kiểm tra lại xem dãy số đó có thực sự là cấp số cộng hay không.
Xác định công sai d của cấp số cộng
Công sai d là số không đổi được cộng vào mỗi số hạng để tạo ra số hạng kế tiếp trong dãy. Bạn có thể tìm d bằng phép tính: d = u2 - u1 hoặc tổng quát là d = u(k) - u(k-1). Khi áp dụng công thức tính tổng dãy cấp số cộng, nếu d lớn hơn 0, ta có dãy số tăng, và nếu d nhỏ hơn 0, ta có dãy số giảm. Việc xác định đúng dấu của d sẽ ảnh hưởng trực tiếp đến độ chính xác của tổng Sn mà bạn đang tính.
Tìm số hạng thứ n bất kỳ trong dãy
Đôi khi đề bài yêu cầu tính tổng nhưng lại giấu đi giá trị của số hạng cuối cùng un. Bạn có thể tìm un dựa vào công thức: un = u1 + (n - 1) * d. Sau khi tìm được un, bạn có thể quay lại áp dụng công thức tính tổng dãy cấp số cộng một cách dễ dàng. Sự liên kết chặt chẽ giữa các công thức thành phần này tạo nên một hệ thống kiến thức logic, giúp bạn giải quyết được cả những bài toán phức tạp nhất.
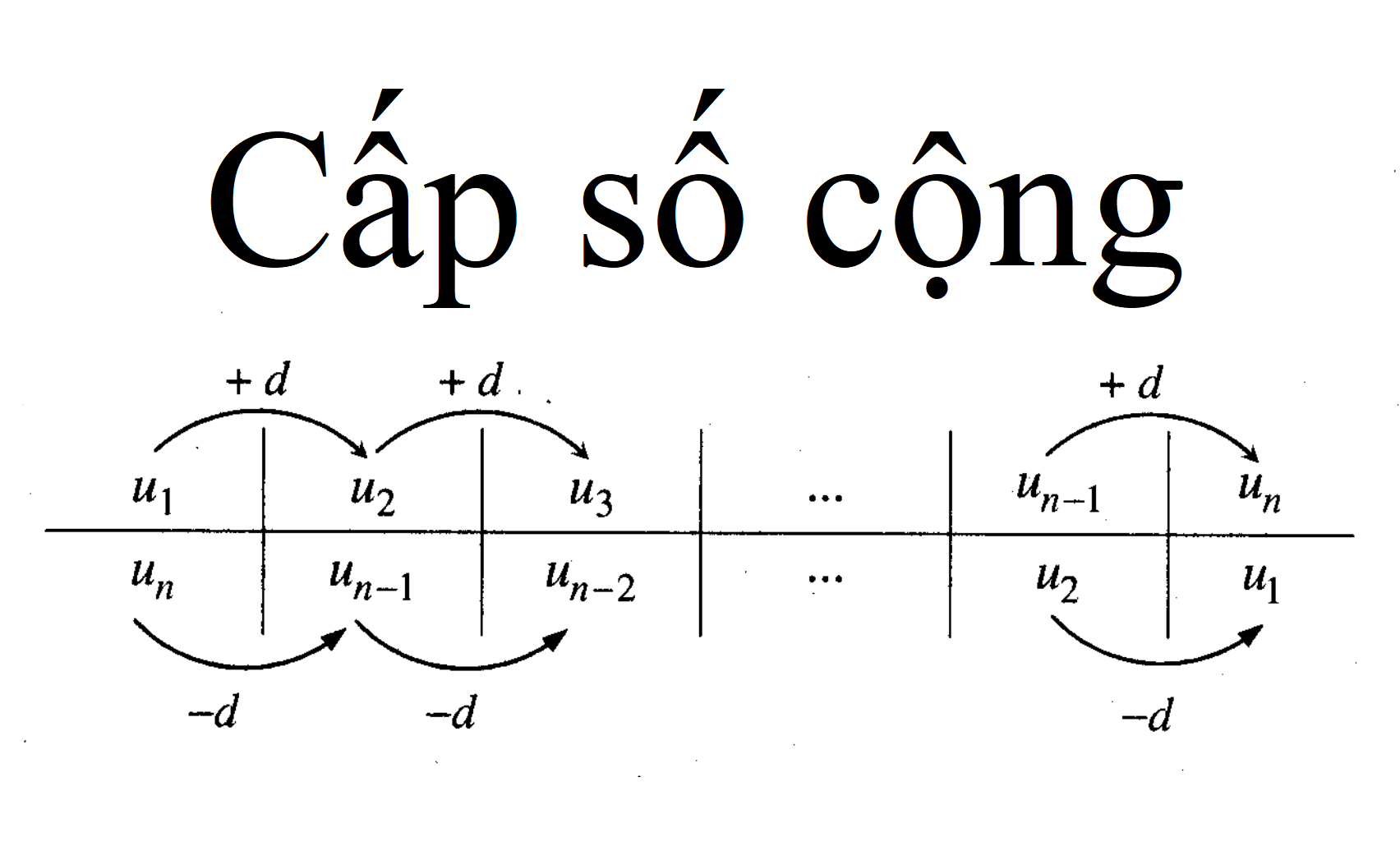
Các thành phần cơ bản cấu tạo nên một bài toán tính tổng cấp số cộng
Dạng bài tập phổ biến nhất là tính tổng của một dãy số tự nhiên cách đều trong một khoảng cho trước. Ví dụ, tính tổng các số lẻ từ 1 đến 99, đây chính là một cấp số cộng với u1 = 1, un = 99 và d = 2. Sử dụng công thức tính tổng dãy cấp số cộng, bạn sẽ nhanh chóng tìm ra kết quả mà không cần cộng từng số một cách thủ công. Dạng bài này thường xuất hiện trong các đề kiểm tra năng lực tư duy toán học cơ bản.
Bài toán ngược tìm số hạng đầu hoặc công sai
Ở cấp độ nâng cao hơn, bạn có thể gặp bài toán cho biết trước tổng Sn và yêu cầu tìm u1 hoặc d. Đối với dạng này, bạn cần thay các giá trị đã biết vào công thức tính tổng dãy cấp số cộng để thiết lập một phương trình. Kỹ năng giải phương trình và biến đổi biểu thức là rất cần thiết để tìm ra các đại lượng còn thiếu. Đây là cách tuyệt vời để rèn luyện khả năng tư duy ngược và xử lý vấn đề một cách linh hoạt.
Ứng dụng cấp số cộng trong đời sống
Cấp số cộng không chỉ tồn tại trong sách giáo khoa mà còn hiện diện trong nhiều tình huống thực tế như tính tiền lãi tiết kiệm, sắp xếp hàng ghế trong rạp hát hoặc tính toán vật liệu xây dựng. Việc sử dụng công thức tính tổng cấp số cộng giúp con người lập kế hoạch và dự toán ngân sách một cách khoa học. Hiểu được ứng dụng thực tiễn sẽ giúp học sinh cảm thấy môn Toán trở nên gần gũi và thú vị hơn rất nhiều.

Quy trình các bước giải một bài toán cấp số cộng từ cơ bản đến nâng cao
Một lưu ý nhỏ nhưng cực kỳ quan trọng là luôn phải kiểm tra điều kiện của dãy số trước khi áp dụng công thức. Công thức tính tổng cấp số cộng chỉ có hiệu lực khi khoảng cách giữa các số hạng là một hằng số d duy nhất. Nếu khoảng cách này thay đổi, dãy số đó không còn là cấp số cộng và việc áp dụng công thức sẽ dẫn đến đáp án sai. Do đó, hãy luôn kiểm tra ít nhất ba số hạng đầu tiên của dãy để xác nhận quy luật.
Tránh nhầm lẫn giữa n và un
Rất nhiều học sinh thường nhầm lẫn giữa vị trí của số hạng (n) và giá trị của số hạng đó (un). Trong công thức tính tổng cấp số cộng, n phải luôn là một số nguyên dương vì nó đại diện cho số lượng phần tử. Trong khi đó, un có thể là bất kỳ số thực nào, tùy thuộc vào đặc điểm của dãy số. Việc phân biệt rõ ràng hai khái niệm này sẽ giúp bạn tránh được những lỗi sai đáng tiếc trong quá trình làm bài thi.
Mẹo ghi nhớ công thức nhanh chóng
Để ghi nhớ công thức tính tổng dãy cấp số cộng lâu hơn, bạn có thể học thuộc lòng câu nói: "Tổng bằng số số hạng nhân với trung bình cộng của số đầu và số cuối". Cách diễn đạt bằng lời này giúp bộ não ghi nhớ bản chất của phép tính Sn = n * (u1 + un) / 2 một cách tự nhiên. Khi đã hiểu bản chất, bạn sẽ không còn lo lắng về việc quên công thức mỗi khi bước vào phòng thi hay khi cần tính toán nhanh trong đời sống.
Thành thạo công thức tính tổng dãy cấp số cộng là một kỹ năng toán học quan trọng, giúp bạn giải quyết nhiều dạng toán từ đơn giản đến phức tạp. Việc hiểu rõ cách xác định n, u1, un và d sẽ tạo nền tảng vững chắc để bạn học lên các phần cao hơn như cấp số nhân hay dãy số vô hạn. Hãy thường xuyên luyện tập các dạng bài tập khác nhau để ghi nhớ công thức một cách bền vững. Chúc bạn luôn tìm thấy niềm vui và đạt kết quả cao trong quá trình chinh phục môn Toán học.